The Power Of Dot Product In Game Development
Math has always been a difficult subject, we all had difficulties studying math at some point, however, we all agree that math is the nature of everything, it’s extremely important in a wide range of fields like engineering, natural sciences, medicine, computer science, and the list goes on.
In the area of game development, math is the essence of any successful game, whether it was simple or much more sophisticated like any AAA game, you would find it used considerably to perform all kinds of tasks, such tasks could be something like character movement, camera controllers, AI systems, or any kind of game mechanics like jumping, dashing or in more advanced ones like climbing systems. It’s essential to the production of any game.
For an instance, you might want to rotate an NPC “non-playable character” to keep looking at a specific target whenever he/she moves, in effect, this is one of the many examples where you would take advantage of the simplicity of the Dot Product to calculate the right angle to rotate your NPC towards.
1. What is the Dot Product? and how can we calculate it?
Mathematically, the dot product aka the scalar product can be defined in two different ways described as follows:
Algebraic definition
Let’s consider it in 3D space, it’s the sum of the products of the corresponding entries in two vectors and it’s written using a central dot i.e.
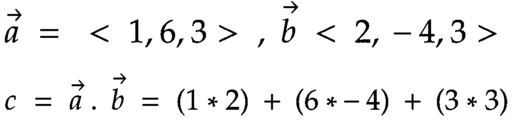
The result of performing the dot product on the above two vectors is a scalar with a value equal to -13. But what does that mean, and how can we make use of this information?. For starters, the number isn’t that important in this case, so it’s better to work with normalized vectors before calculating the dot product.
To normalize a vector simply means to take a vector of any length and change it to 1, surely it still pointing in the same direction as it was before, it only becomes of length 1, this is called a unit vector. To get the unit vector for any given vector you simply divide each entry by the magnitude as follows:

Therefore, after normalizing the two given vectors that were mentioned previously (a & b) now we can calculate the dot product again to get a scalar with a value equal to -1.
Calculating the dot product between normalized vectors will yield a value in the range of [-1,1].
- -1 → means that the angle between the two vectors is greater than 90 degrees.
- 0 → means that the angle between the two vectors is exactly 90 degrees, indicating that they are perpendicular to each other.
- 1 → means that the angle between the two vectors is less than 90 degrees.
knowing only this simple information we can determine if a character is in a front of an NPC or behind him.

Notice how the dot product result changes when the player moves from rear to side and then to the front of the NBC.
2. Using the dot product to get the angle between two vectors
Let’s consider a game where you have a Tank and you want its turret to keep looking at a specific target or maybe an AI agent that you want to stay put in some predefined place and once the target has been spotted you want him to start shooting while keeping an eye on that target whenever he/she moves, surely there should be a limit to the AI vision, or you might want to define a region such as a cone, it’s very popular in AAA games that they define a cone which an NPC can only attack the player if it has been detected in that region, so let’s see how we can do that.
Geometrically
The dot product between two vectors can be defined as follows:
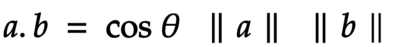
Thus, to get the angle theta we can simply take the inverse cosine or as called the arc cosine of the dot product of the two vectors a and b divided by the multiplication of their magnitudes.
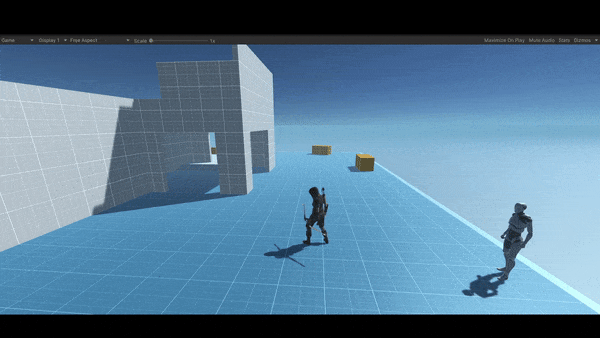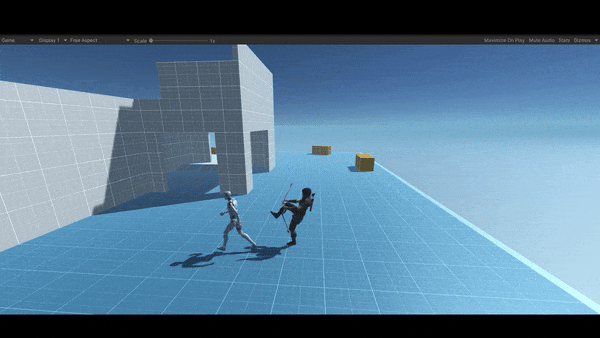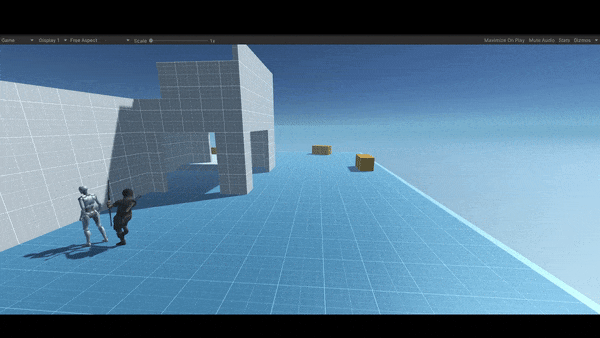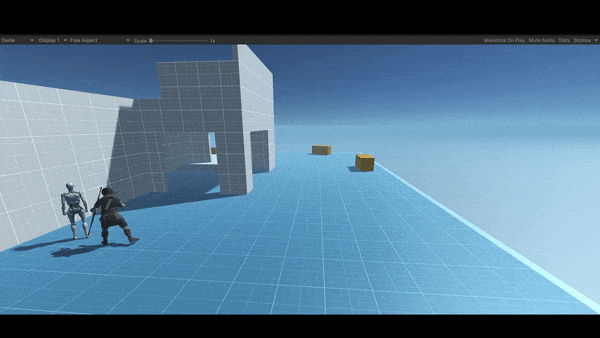
Here is a simple implementation of an AI line of sight “Cone Detection“ in Unity 3D. By the way, this is just an explanation, you can find the source code and all the related project files in the resources section at the end of the article.
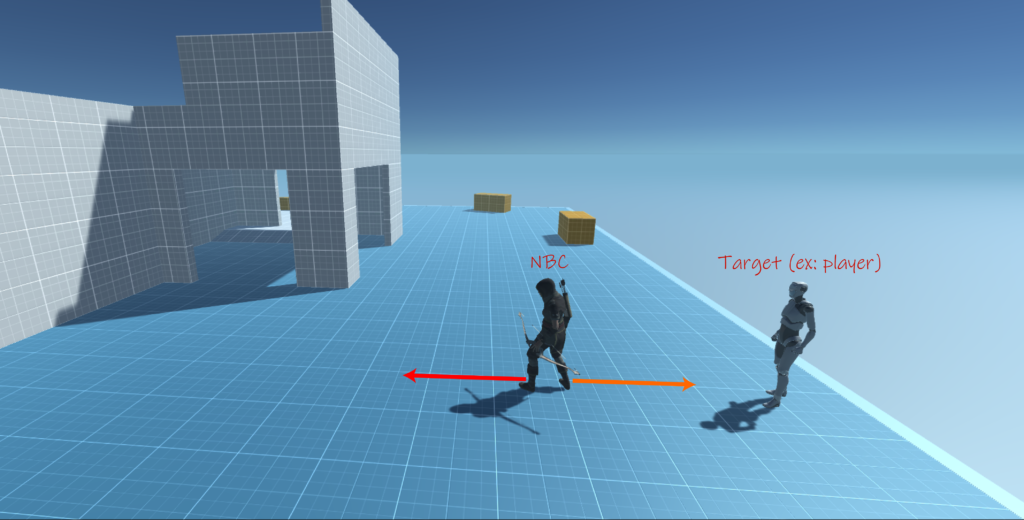
In the above image as you can see the target is behind the NBC and since the NBC forward vector “red arrow” points towards the forward axis “in Unity3D it’s the z-axes” and the direction vector “orange arrow” that points towards the target is in the opposite direction, so that makes the NPC unable to detect the target as long as he stays behind her, though you can do that if that is the case in your game by simply increasing the range of the angle theta to 180 degrees.
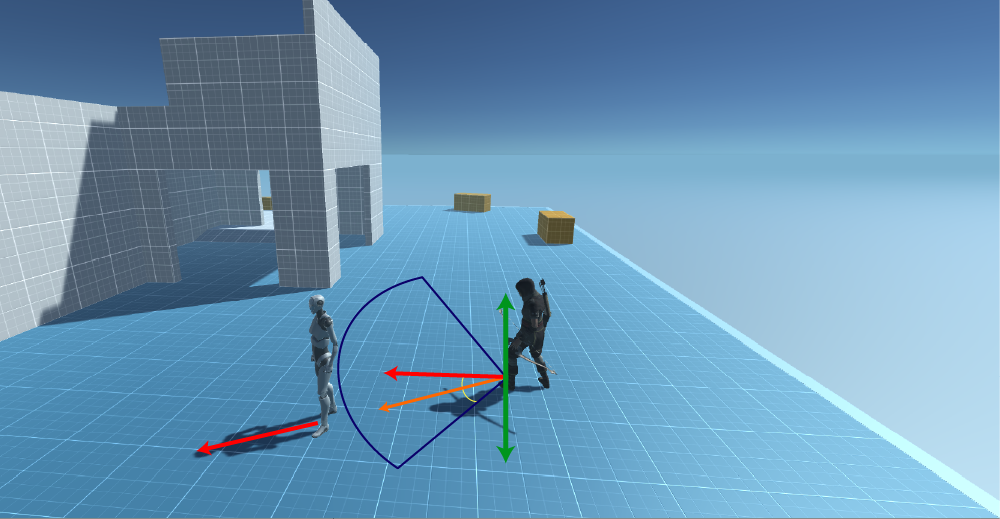
Yet if you take a look at the second image you will see that now the NBC can detect the player since he is in the range of her vision, and that can be determined by defining a cut-off angle, in this case, I defaulted it to 45 degrees. The angle is calculated from the NBC forward vector to the direction, where the direction is the distance from the target to the NBC.
After detecting the target, now the ball is in your court, you can do just about anything, for an instance make the NBC run after him, attack him, throw a grenade at him, shoot an arrow from distance, or maybe get in a fight with him, in this simple example once the NBC spot the target she starts chasing him and once she gets in a small distance from the player she starts attacking him (just playing a simple attack animation), by the way, this small distance called the stopping distance.
3. The projection of one vector onto the other
Lastly, I am going to talk briefly about how can we use vector projection to find a force, which is one of the most known applications of the dot product.
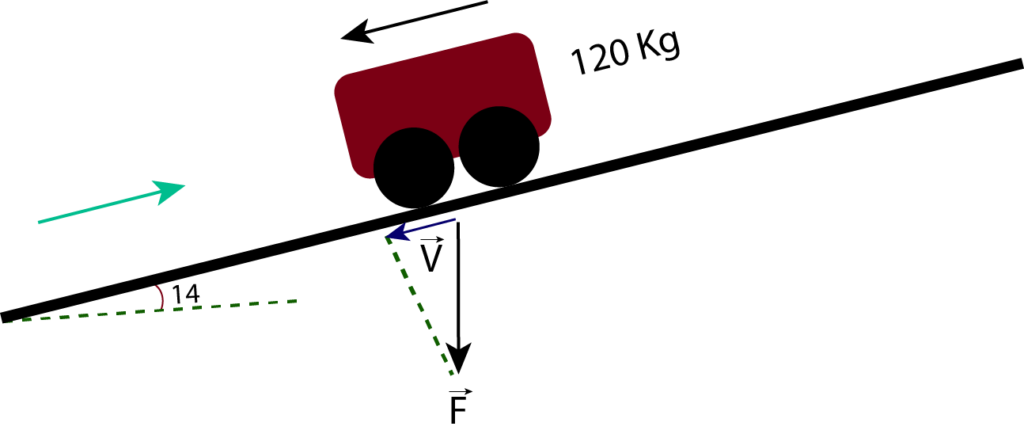
A very common problem in physics is where you have to figure out how much force you need to push in the opposite direction of a cart, boulder, or even a car to stop it from rolling down a hill. Look at the image down below.
Initially, let’s see the formula that we will be using to find the projection of one vector onto the other.
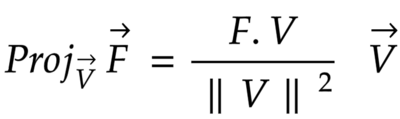
you can see that the projection of vector F onto vector V it’s simply a scalar amount of vector V. Therefore, back to the image if we were to project vector F which is the gravitational force that is applied on the cart or vector V as denoted by the dark blue arrow, you may have noticed that V is a unit vector and that only to make the calculation simpler since we know beforehand that the projection of vector F onto V is a scalar amount of it and that is all that we are after in this case, because remember we need to find the desired magnitude to push in the opposite direction, so let’s begin by writing down the vectors in a component form.
F is the gravitational force (F = m * a) in newton, where m is the mass of the cart which is 120 Kg, and a, in this case, is the acceleration of gravity denoted as g = 9.8 m/s2 and since it’s a downward force we can write it as
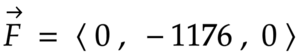
, we can write V in the form of sine and cosine for we already know that the ramp or the hill is tilted by 14 degrees thus it becomes
, vector V is a unit vector which means that its magnitude equals 1. As a result of calculating the dot product of the two vectors F and V, we get a value equal to -284.5, Finally, let’s plug all these values into the equation:
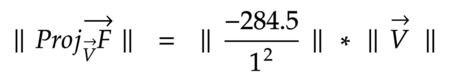
F = -284.5 N is the right amount of force that is required to stop the cart from rolling down the ramp, back to newton’s second law 284.5 = m * 9.8, we get m equal to 29 Kg, which means we don’t need the whole 120 Kg to stop the cart from rolling down the ramp.
This is how it looks in Unity3D

Resources
The source code and all the related project files on GitHub → Dot Product
